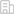水在寒冷的冬天会结冰、被加热后会发生汽化,这是人们日常生活中常见的现象。物质的状态在物理学中被称为“相”,比如水有固相、液相和气相等,而物质从一种相转变为另一种相的过程就是“相变”(Phase transition)。
与水的“相变”相比,有一些“相变”令人着迷:比如铁在加热到770度时会失去铁磁性,超导材料在极低温下会出现的超导性质。这个过程中究竟发生了什么?
物理学家尝试通过建立数学模型来寻找答案。100年前诞生的著名的“伊辛模型”,就是解开相变问题的一把“数学钥匙”,但至今有许多问题悬而未决。
最近,西湖大学理学院朱伟团队在这一经典问题上取得重大进展。他们提出了一种新的理论方法用以研究三维伊辛模型,通过巧妙地设计量子化方案,在二维球面几何上实现了量子相变,并成功揭示了相变点的共形场特征。
这一研究成果引起各国物理学家的广泛关注。以该成果为专题的第一个学术研讨会“Fuzzy sphere meets bootstrap”将于今年11月在美国召开。
该研究由西湖大学强关联与拓扑物性课题组完成,在Physical Review X 以及Physical Review Letters 连续发表两篇研究论文。西湖大学理学院朱伟为第一篇论文的第一作者,博士后韩超为第二作者;博士后胡樑栋为第二篇论文第一作者;西湖大学理学院朱伟与加拿大圆周研究所研究员何寅琛同为两篇论文的通讯作者。
01“最 难 ”求 和
1895年,居里夫人的先生——皮埃尔·居里(Pierre Curie)在实验中发现,磁铁加热到一定温度,会突然失去磁性。相变发生前后,物质的化学构成并没有变化,但物理性质却大相径庭。并且这些相变都会有一个明确的“临界点”,我们称之为相变点。
对相变的数学模型的理论研究,正是从铁磁性开始的。
25年后,德国物理学家威廉·楞次(Wilhelm Lenz)接过这一棒,当时世界正从一场大流感中复苏。他把铁磁性材料抽象成由一个个“原子”构成的晶格,每一个“原子”都有或向上或向下的指向,称为“自旋”。自旋之间的相互作用使得自旋倾向于同向排列,从而使得整个材料呈现出铁磁性;另一方面,由于热运动的影响,自旋的指向会倾向于变得无序。因此,自旋之间的相互作用和温度便产生了竞争关系,这种竞争关系导致了铁磁体的相变,那么应该如何来描述这种竞争呢?

楞次(左)和伊辛 (右)
楞次把接下来的工作交给了他的学生伊辛(Ernst Ising)。理论上,每一个自旋的状态,可以用1或者-1来描述——代表向上或者向下,并且相邻的自旋会相互影响,趋向于保持一致。1924年,伊辛把原子模拟成格点,写下了这个著名的公式,在数学上构建了一个微观变化如何影响到宏观性质的模型:
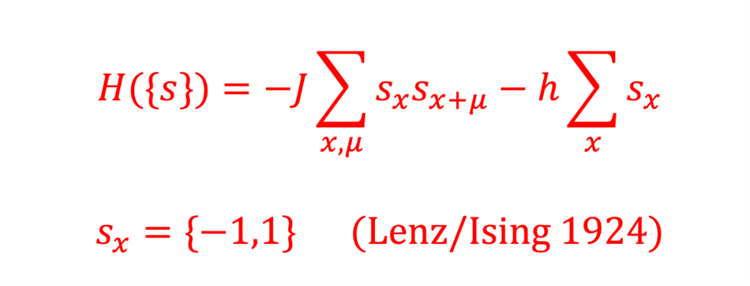
H代表哈密顿量,描述系统的总能量。左边包含-J的项描述了系统中自旋相互作用的能量,包含-h的项描述外部磁场对自旋的影响。J是描述自旋之间相互作用的参数,h是一个和外部磁场相关的参数。
而温度的影响就需要通过热涨落来刻画,因此需要将上面的公式对所有可能的自旋构型进行求和。而这一求和过程却极其困难,被戏称为“最难的求和”。其原因来源于系统总的自旋构型数目是一个天文数字。虽然模型中一个格点只有两种构型(朝上或者下),但随着格点的数目的增加,总的系统构型数目会指数增长:例如对于一个只有256个格点的系统,总的状态数就达到了2的256次方,大概是宇宙中能观察到恒星数的3.5倍。
一维伊辛模型的示意图
图源作者 Yaël L. Birenbaum Haligua
伊辛只能先尝试把这个模型在一维来研究,将其简化成一个环形的箭头链,每一个箭头都可以“感知并影响”周围两个相邻的“邻居”,并由此求得了一维伊辛模型的解析解。可惜,在一维情况下,相变温度是热力学绝对零度,这与实际三维材料中所观察到的现象不一致。伊辛和导师楞次试图把模型推广至二维和三维,都以失败告终。
但是,伊辛模型所折射出的数学魅影,不断吸引了后续的研究者。凝聚态物理学家约翰·贝林斯基如此妙语点评一维伊辛模型:“一维只是没有它所需要的东西。”
02万 物 皆 数
时间来到了二十世纪四十年代,物理学家、诺贝尔奖得主拉斯·昂萨格(Lars Onsager)对伊辛模型产生了兴趣。他把磁铁简化成一个类似于围棋棋盘的二维模型。此时,每一个格点需要考虑前后左右四个相邻格点的影响,计算量也扶摇直上。

二维伊辛模型示意图:实际上,在模型的构建中,格点的数目可以趋于无穷大。图源:research gate
1944年,拉斯·昂萨格宣布求得二维伊辛模型的解析解,这里先略去复杂的数学求解过程,昂萨格的工作证明了二维伊辛模型存在非零温的相变点,这说明了相变过程可以用二维伊辛模型解释,而不需要像当时很多物理学家认为的那样,需要考虑到真实粒子的相互作用。
但这个理论似乎过于简化,它能模拟现实吗?很快,来自实验物理的数据点亮了这个模型。科学家们通过对氩和氦的测定,发现这些物质的“临界指数”和拉斯·昂萨格计算的解完美吻合,这些指数是1/8或者7/4这样的数字,它描述了相变前,例如像热容等各种物理量在临界点附近的变化速度。
一系列不相关的物质,不管是由铁原子、水分子还是理论模型中虚拟的格点构成,在相变发生时,都有着相同的临界指数,这就说明伊辛模型具有普适性。
后续科学家继续持续接力,不断发掘着伊辛模型背后的惊人规律。1970年,物理学家亚历山大·波利亚科夫(Alexander Polyakov)证明了,二维伊辛模型在其临界点会表现出共形不变性。什么是共形不变形?你可以这样理解,不管你如何平移、缩放、旋转这个系统,整个系统都是不变的。这就意味着在相变发生的时候,不论微观细节如何变化,系统的全局行为也不会改变。
而这些神奇的特性,在相变点前或者后都是不存在的。
在波利亚科夫的开创性工作之后,人们纷纷猜测解决三维伊辛模型的关键就是共形不变性,但是,三维伊辛模型的共形不变性至今缺乏严格证明。虽然在这条漫长的探索之路上不乏新的进展,例如,2018年,当时年仅33岁的的法国数学家雨果·迪米尼-科潘(Hugo Duminil-Copin)证明了三维伊辛模型存在连续相变,这一进展被授予2022年菲尔茨奖。
“伊辛模型”因其展示了系统中个体状态与宏观状态之间的关系而获得了巨大的吸引力。实际上,这一模型已经进入到多个自然科学领域的研究中,不再局限于物理领域,包括了DNA的折叠、病毒的传播以及大脑神经细胞的激活与不激活状态等。这些研究中都存在着有序与无序的相变和临界现象。
此外,伊辛模型还推动了社会物理学和经济物理学的发展,因为社会和经济行为同样由众多个体组成,这些个体之间相互影响,并受到宏观因素的影响。
03世界是圆的,吗?
2018年,朱伟加入西湖大学理学院,建立了“强关联和拓扑理论实验室”。他本科和博士均毕业于中科大,之后分别在美国加州州立大学北岭分校、普林斯顿大学、洛斯阿拉莫斯国家实验室从事博士后研究,主要聚焦强关联体系中的拓扑有序相、量子纠缠在多体物理中的应用等方向。
在以往的研究中,不论是二维还是三维的伊辛模型,都是在平直空间内建立的。平直空间指的是我们熟悉的欧式几何中的二维平面和三维空间。有趣的是,尽管已经在平直空间下构建了三维伊辛模型,但目前尚未观察到该模型具备共形不变性的明确特征。
也许,平直空间不是构建伊辛模型“最优方法”?那会是什么?从2019年开始,朱伟就一直在思考这个问题。一个可能的思路是,通过构建一个量子化的伊辛模型,在一个不同于平直时空的数学流形上去研究相变的物理性质。
相变从分类上,大致可以分为经典相变和量子相变。通俗的解释,经典相变是热涨落引起的,而量子相变发生在热力学绝对零度时。虽然绝对零度是无法达到,但随着温度降低,组成物质的原子或者分子的热运动被逐渐冻结,量子涨落效应开始占主导作用,从而诱导一些全新的量子态或者量子临界现象,这就是量子相变。
在数学上,用于描述量子相变系统内个体的方式不仅仅局限于粒子自旋只有1和-1两种状态,还包括了这些状态的叠加态。朱伟团队及其合作者构建了一个三维伊辛模型,旨在模拟量子相变现象,他们在这一工作中融合了传统伊辛模型的概念,考虑了粒子之间的相互作用以及横向磁场对系统的影响,同时也采用了独创性的方法来构建这个模型。
为了避免深入复杂的数学描述和推导,我们仅简要概述这一理论模型的构建方式:研究团队将经典的伊辛模型映射到一个二维球面上,并创建了一个(2+1)维时空的量子伊辛模型。
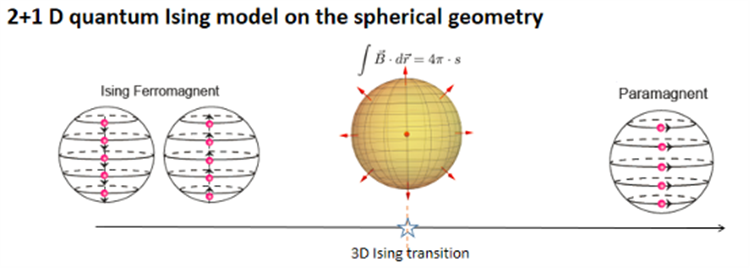
朱伟和合作者在球面几何上构造的2+1维度的量子伊辛模型
在以往的研究中,伊辛模型的定义一直面临着需要引入短程截断的问题,通常需要使用晶格结构来解决。然而,这项研究采用了一种全新的量子化方法,以避免这一问题。具体来说,他们在球心处放置了磁单极,并考虑了带电粒子在球面上的运动,这个方法被称为“Fuzzy Sphere”正规化。该方法以一种完全不同但却更具对称性的方式定义了一个有限的模型。
最令人惊讶的是,这种正规化的方法在有限系统尺寸下给出了近乎准确的结果。通过与共形场论的理论预言进行比较,发现两者达成了惊人的一致性。更为重要的是,该工作还获得了一些共形场论相关的其他数值计算方法暂时未能给出的新结果。这说明了这一理论方法不是简单地重复或重现一些已知的结果、或对以前方法的简单补充,而是一种功能强大的、崭新的方法,可以发现一些尚未知晓的物理信息,并拓展到更多相变普适类的研究中去。
复杂体系中大量自由度的相互作用为我们带来了丰富多彩的世界。而在纷繁的复杂体系中提炼简洁、优雅却又不平凡的规律是人类探索自然的永恒课题。临界现象及其背后的普适规律正是一个值得深入探索的领域。统计物理模型则是物理学家研究这一领域的关键工具。因此,研究统计模型对于推动这一领域的发展具有重要意义。“Fuzzy Sphere”方案正是从一个全新的视角来研究一类重要的统计物理模型,不仅解决了模型中的诸多困难,还为我们深入理解临界现象打开了一个新的维度。